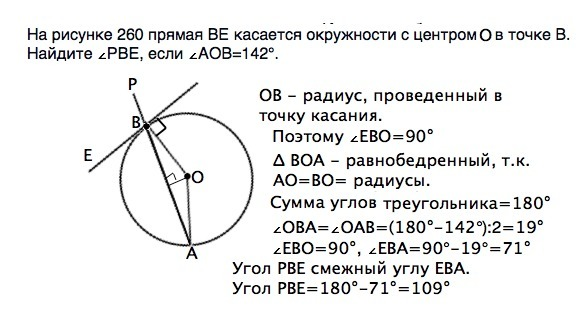
На рисунке 160 прямая ВЕ касается окружности с центром О в точке В. Найдите ∠РВЕ, если ∠АОВ=142°
–––––––
ОВ - радиус, проведенный в точку касания.
Поэтому ∠ЕВО=90°
∆ ВОА - равнобедренный, т.к. АО=ВО= радиусы.
Сумма углов треугольника=180°
∠ОВА=∠ОАВ=(180°-142°):2=19°
∠ЕВО=90°, ∠ЕВА=90°-19°=71°
∠ РВЕ смежный углу ЕВА.
∠ РВЕ=180°-71°=109°