4. График линейной функции - прямая. Прямую можно задать двумя точками, которые связаны формулой:
(у-у1)/(у2-у1)=(х-х1)/(х2-х1).
Точки прямой: (0;-4) и (-2;2).
Подставляем в формулу:
(у+4)/(2+4)=(х-0)/(-2-0);
(у+4)/6=х/-2;
-2(у+4)=6х;
-2у-8-6х=0;
-6х-2у-8=0.
Уравнение прямой у=kx+b, можно из полученного равенства выразить у:
-2у=6х+8;
у=(6х+8)/-2=-3х-4.
у=-3х-4.
Можно найти формулу другим способом:
Точки прямой: (0;-4) и (-2;2).
Уравнение прямой у=kx+b. Имеем два неизвестных компонента: k и b.
Подставляя в уравнение прямой координаты точек, получаем систему уравнений:
(1) -4=k*(0)+b, ⇒ b=-4,
(2) 2=k*(-2)+b; ⇒ 2=-2k-4 ⇒ -2k=6 ⇒k=-3.
Таким образом, уравнение прямой у=-3х-4.
Находим значение функции при х=-0,987:
у=-3*(-0,987)-4=2,961-4=-1,039.
Ответ: -1,039.
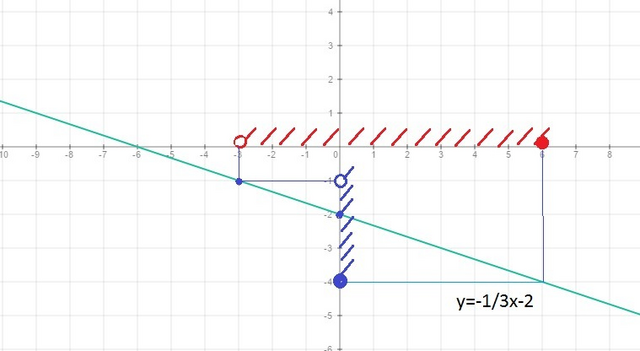
8. у=-1/3х-2.
График линейной функции - прямая, прямую можно построить по двум точкам. Составляем таблицу:
х у
0 -2
-3 -1
Наносим эти точки на координатную плоскость и проводим через них прямую. Эта прямая и будет графиком данной функции.
При -4≤y<-1 x∈(-3;6], или -3<x≤6.<br>См. рисунок.