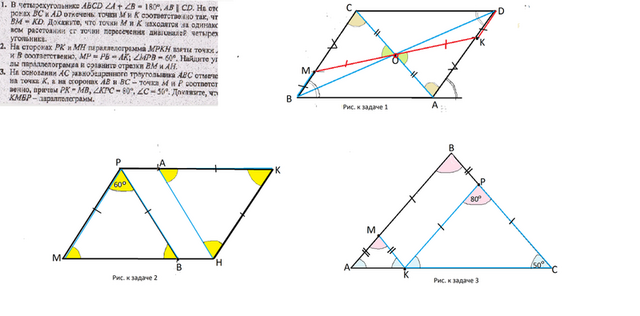
1.В четырехугольнике АВСD ∠А+∠В=180°, АВ||CD. На сторонах ВС и АD отмечены точки М и К соответствеенно так, что ВМ=КD.Докажите, что точки М иК находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
По условию ∠А+∠В=180°.
Так как эти углы лежат на одной прямой и являются односторонними, ВС||AD по свойству углов при двух прямых и секущей. АВ||CD. Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
АВСD - параллелограмм. Противоположные стороны параллелограмма равны, противоположные углы параллелограмма равны, диагонали параллелограмма точкой пересечения делятся пополам.
В треугольниках СОМ и АОК стороны СО=ОА, углы СОМ=КОА как вертикальные, Углы МСО=КАО как накрестлежащие при ВС и АD.
Если в треугольниках сторона и прилежащие к ней два угла равны, то эти треугольники равны.
=>МО=ОК, что и требовалось доказать.
2.
На сторонах РК и МН параллелограмма МРКН взяты точки А и В соответственно, МР=РВ=АК; ∠МРВ=60°. Найдите углы параллелограма и сравните отрезки ВМ и АН.
По условию МР=РВ, и угол МРВ равен 60°.
Этот треугольник не просто равнобедренный, но равносторонний, т.к. все углы в нем равны 60°(проверьте).
Следовательно, острые углы параллелограмма равны 60°,
тупые=180°- 60°=120°.
МР=РВ=АК, но РМ=КН как противоположные стороны параллелограмма.
Треугольник АКН - равносторонний. АН=ВМ.
3.
На основании АС равнобедренного треугольника АВС отмечена точка К, а на сторонах АВ и Вс - точки М и Р соответственно, причем РК=МВ, ∠КРС=80°, ∠С=50°. Докажите, что КМВР - параллелограмм.
Треугольник АВС по условию равнобедренный.
Следовательно, ∠А=∠С=50°, угол при вершине В равен углу КРС=80°
В треугольнике КРС угол при вершине Р=80°, угол при С равен 50°, третий его угол при К=180°-80°-50°=50°.
Треугольник КРС - равнобедренный.
Т.К. ВМ=КР, то РС=ВМ.
Если от равных сторон АВ и ВС отрезать равные отрезки, оставшиеся части сторон также равны.
АМ=ВР.
Но треугольник АМК - равнобедренный ( сможете доказать самостоятельно по углам).
В четырехугольнике КМВР противоположные стороны попарно равны.
Этого достаточно,чтобы доказать их параллельность, хотя можно подкрепить доказательство ещё и равенством углов. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
Рисунки к задачам даны во вложении, все равные углы на них окрашены одинаковым цветом.