Можно через площадь треугольника))
S = p*r = ab / 2
(площадь описанного многоугольника (не только треугольника) = произведению полу-периметра на радиус вписанной окружности,
площадь (только) прямоугольного треугольника = половине произведения катетов)))
(a+b+c)*r = a*b
r = a*b / (a+b+c)
с = √(12²+5²) = 13
r = 5*12 / (5+12+13) = 5*12 / 30 = 2
------------------------------------------------
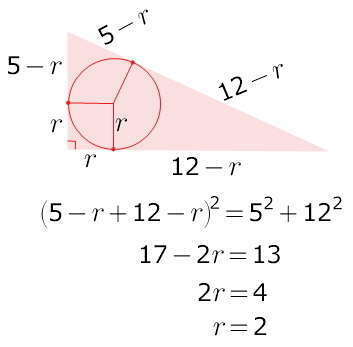
можно, составив уравнение)))
для этого нужно вспомнить, что отрезки касательных, проведенных из одной точки к окружности, равны;
что радиус, проведенный в точку касания, перпендикулярен касательной;
вписанная в прямоугольный треугольник окружность "вырезает" из прямого угла квадрат своими радиусами...