Чтобы ИЗМЕРИТЬ расстояние между двумя точками, надо провести между ними прямую и измерить длину отрезка между этими точками.
Геометр, расставляя точки на окружности получил вписанный многоугольник.
Формула КОЛИЧЕСТВА диагоналей многоугольника:
K=n*(n-3)/2.
Расположив, к примеру, 6 точек на окружности, он получил шестиугольник с 9 диагоналями, да еще 6 сторон - итого 15 отрезков, которые он измерил. Предположим, что все отрезки разные.
Значит, для получения 15 разных чисел он расставил 6 точек.
Но предположим, что многоугольник получился правильным.
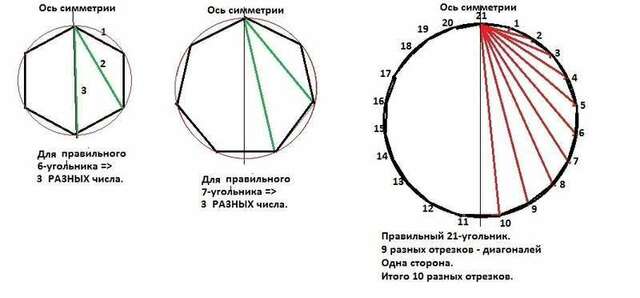
И тогда мы увидим, что РАЗНЫХ чисел у геометра получилось только 3 сторона (все стороны равны) и две диагонали (все остальные попарно равны измеренным двум). Получилось так потому, что правильный n-угольник имеет n осей симметрии, проходящих через его центр.
Если n - четно, то оси симметрии правильного многоугольника содержат
противоположные вершины.
Если n - нечетно, то осями симметрии правильного многоугольника являются прямые, каждая из которых проходит через вершину многоугольника перпендикулярно противолежащей ей стороне.
Проведем ось симметрии для нашего 6-угольника. Она пройдет через ЛЮБЫЕ две противоположные вершины и окажется, что две вершины, лежащие по разные стороны оси симметрии, равноудалены от вершины, через которую проходит ось симметрии, но имеют разную длину.
Один из этих отрезков в 6-угольнике совпадает со стороной 6-угольника и его не считаем. И плюс расстояние между противоположными вершинами. Итого 2 разных отрезка. Да еще отрезок - сторона многоугольника. Итого 3 РАЗНЫХ отрезка.
Рассмотрим правильный 7-угольник, у которого ось симметрии пройдет через вершину и середину противоположной стороны. Мы получим те же 2 разных отрезка по одну из сторон оси симметрии плюс отрезок - сторону. Итого - те же 3 разных отрезка.
Итак, построив правильный 7-угольник, мы получили 3 разных отрезка или наоборот, чтобы получить 3 разных числа (отрезка) нам пришлось построить правильный 7-угольник.
Получили формулу: О=(n-1)/2, или наоборот, n=2*O+1,
где О - максимальное количество разных отрезков.
Так как геомтру необходимо получить МАКСИМАЛЬНОЕ число точек, то для получения 40 РАЗНЫХ чисел ему понадобится расположить на окружности 81 точку, построив ПРАВИЛЬНЫЙ 81-угольник.
P.S. Строить правильный 81-угольник сложно. На рисунке для примера дан 21-угольник. Для проверки формулы можете легко построить 8 и 9-угольники или 10 и 11 угольники и сравнить их.