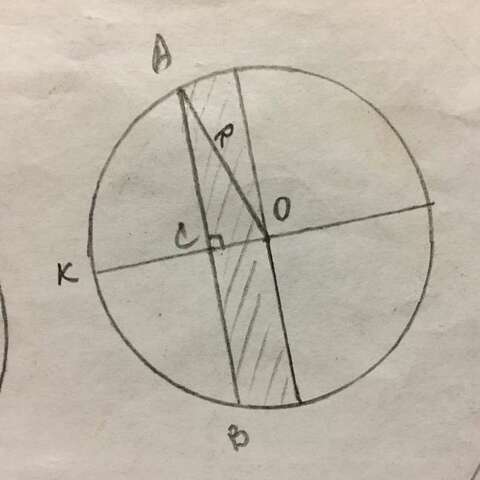Есть три отрезка диаметра, значит имеем две точки деления. Сумма первых двух отрезков относится к третьему как 3:3, значит вторая точка делит диаметр пополам, а первая точка делит радиус в отношении 2:1.
Чтобы получить объём шарового слоя нужно от половины объёма шара вычесть объём шарового сегмента, определённого хордой АВ как диаметром сечения.
Объём половины шара: Vп=V/2=4πR³/6=2πR³/3
Объём шарового сегмента: Vc=πh²(R-h/3), где h - высота сегмента. h=СК. СК:СО=2:1, КО=R ⇒ CK=2R/3=h.
Vc=π·4R²(R-2R/9)/9=4R³((9-2)/9)/9=28R³/81.
Объём шарового слоя: Vслоя=Vп-Vc=2πR³/3-28πR³/81=26πR³/81 - это ответ.