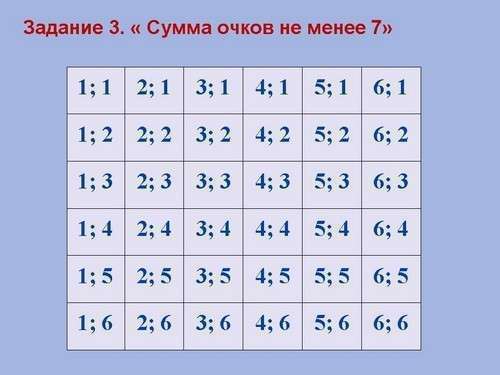
При первом броске выпавшее число может быть от 1 до 6. При втором броске - аналогично.
На прикрепленной картинке представлены все возможные сочетания чисел, выпадающих при броске игральной кости дважды.
Например, "1;1" означает, что оба раза выпало число 1; "3;4" означает, что при первом броске выпало число 3, при втором - 4.
Следовательно, нужно определить, в каких сочетаниях между числами разница составляет 2.
Это можно наблюдать в таких случаях, когда выпадают числа: "1;3", "2;4", "3;1", "3;5", "4;2", "4;6", "5;3", "6;4".
Таким образом, условие задания удовлетворяют только 8 случаев из 36 возможных.
Вероятность определяется через отношение нужных нам событий к числу всех возможных.
Получаем, что вероятность того, что при броске игральной кости дважды выпавшие числа очков будут отличаться на 2, равна:

Это и есть ответ.