Діагональ прямокутного паралелепіпеда дорівнює L і утворює з двома суміжними гранями кути...

Question

Діагональ прямокутного паралелепіпеда дорівнює L і утворює з двома суміжними гранями кути а і b. Знайти об'єм паралелепіпеда

Answer 1

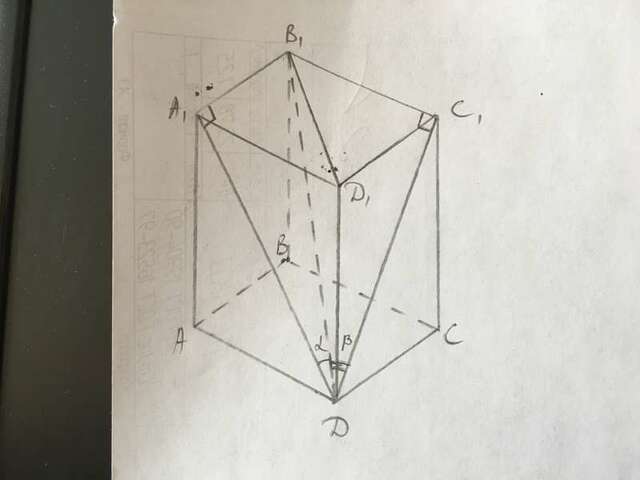
В1Д=L, ∠А1ДВ1=α, ∠ С1ДВ1=β.
V=?

В тр-ке А1В1Д  А1В1=В1Д·sinα=Lsinα.
В тр-ке С1В1Д  В1С1=В1Д·sinβ=Lsinβ.
В тр-ке А1В1Д1 В1Д1²=А1В1²+А1Д1²=L²sin²α+L²sin²β=L²(sin²α+sin²β).
В тр-ке ДВ1Д1 ДД1²=В1Д²-В1Д1²=L²-L²(sin²α+sin²β)=L²(1-sin²α-sin²β)=L²(cos²α-sin²β).
Объём параллелепипеда:
V=abc=А1В1·В1С1·ДД1=Lsinα·Lsinβ·L√(cos²α-sin²β)=L³sinα·sinβ·√(cos²α-sin²β) - это ответ. 

---