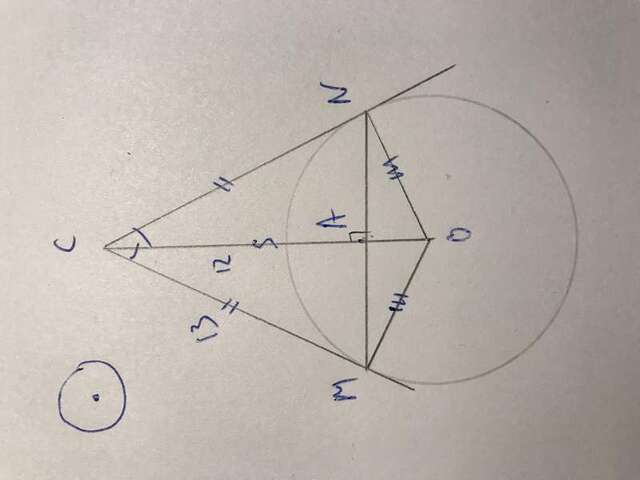
(И=N чтоб языки не переключать) Рассмотрим треугольник СМО и треугольник СИО они равны по трём сторонам, СО общая, СМ равна СИ как касательные, СО рана ОИ как радиусы, отсюда угол МСО равен углу ИСО, следовательно СО биссектриса, рассмотрим треугольник СИМ, он равнобедренный, СО биссектриса, следовательно медиана и высота, отсюда СМА прямоугольный треугольник, МА равно АИ, по теореме Пифагора АМ^2=СМ^2-СА^2, АМ=Корень(169-144) = 5, следовательно МИ=5*2=10
Ответ: 10