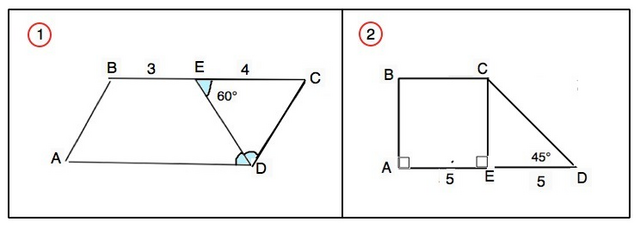
1) В параллелограмме противолежащие стороны равны и параллельны, противолежащие углы равны.
ДЕ - биссектриса, ⇒∠ЕDА=∠ЕDС.
∠СЕD=∠ЕDА – накрестлежащие. ⇒
треугольник СЕD равнобедренный, а так как углы при основании ЕD равны 60°, он - равносторонний.
Угол С=60°, угол А=угол С=60°. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°. ⇒∠В=∠D=120°
СD=ЕС=АС=4 см. АD=ВС=3+4=7 см
Р (АВСD)=2•(7+4)=22 см
Четырехугольник АВЕD - равнобедренная трапеция, так как ВЕ║|АD, и АВ=СД⇒АВ=ЕД.
-------------------
2) ∆ СЕD прямоугольный, Сумма острых углов прямоугольного треугольника 90°. ⇒
угол ЕСD=90°- 45*=45°⇒ ∆ СЕD – равнобедренный.
CE=ED=5
Перпендикуляр СЕ параллелен и равен АВ. -⇒
АВ=СЕ=5 см