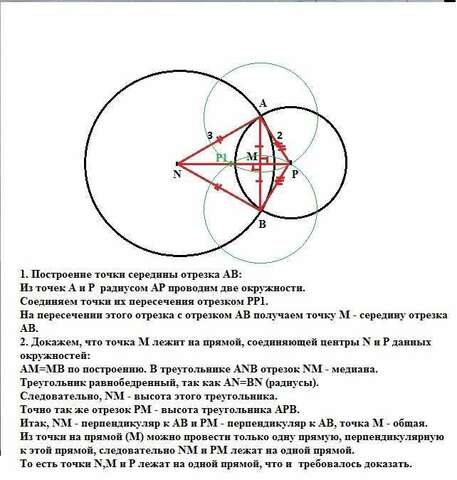
1. Построение точки середины отрезка АВ:
Из точек А и Р радиусом АР проводим две окружности.
Соединяем точки их пересечения отрезком РР1.
На пересечении этого отрезка с отрезком АВ получаем точку
М - середину отрезка АВ.
2. Докажем, что точка М лежит на прямой, соединяющей центры N и P данных окружностей:
АМ=МВ по построению. В треугольнике ANB отрезок NM - медиана.
Треугольник равнобедренный, так как АN=BN (радиусы).
Следовательно, NM - высота этого треугольника.
Точно так же отрезок РМ - высота треугольника АРВ.
Итак, NM - перпендикуляр к АВ и РМ - перпендикуляр к АВ, точка М - общая.
Из точки на прямой (М) можно провести только одну прямую, перпендикулярную к этой прямой, следовательно NM и РМ лежат на одной прямой.
То есть точки N,М и Р лежат на одной прямой, что и требовалось доказать.