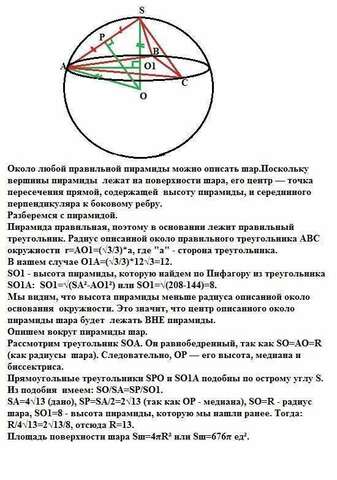
Около любой правильной пирамиды можно описать шар.Поскольку вершины пирамиды лежат на поверхности шара, его центр — точка пересечения прямой, содержащей высоту пирамиды, и серединного перпендикуляра к боковому ребру.
Разберемся с пирамидой.
Пирамида правильная, поэтому в основании лежит правильный треугольник. Радиус описанной около правильного треугольника АВС окружности
r=АО1=(√3/3)*а, где "а" - сторона треугольника.
В нашем случае О1А=(√3/3)*12√3=12.
SO1 - высота пирамиды, которую найдем по Пифагору из треугольника SO1A: SO1=√(SA²-AO1²) или SO1=√(208-144)=8.
Мы видим, что высота пирамиды меньше радиуса описанной около основания окружности. Это значит, что центр описанного около пирамиды шара будет лежать ВНЕ пирамиды.
Опишем вокруг пирамиды шар.
Рассмотрим треугольник SOА. Он равнобедренный, так как SO=AO=R (как радиусы шара). Следовательно, OР — его высота, медиана и биссектриса.
Прямоугольные треугольники SРO и SO1А подобны по острому углу S. Из подобия имеем: SO/SA=SP/SO1.
SA=4√13 (дано), SP=SA/2=2√13 (так как ОР - медиана), SO=R - радиус шара, SO1=8 - высота пирамиды, которую мы нашли ранее. Тогда:
R/4√13=2√13/8, отсюда R=13.
Площадь поверхности шара Sш=4πR² или Sш=676π ед².