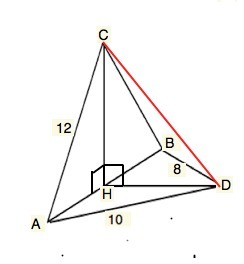
Плоскости ∆ АВС и ∆ АВD перпендикулярны,⇒
высота СН равностороннего ∆ АВС перпендикулярна общей для двух треугольников стороне АВ и медиане AD (т.к. АН=ВН.) треугольника АВD. Следовательно, СD - гипотенуза ∆ СНD/
CD²=CH²+DH²
CH²=(AC•sin60°)²=(12•√3):2)²=108
Формула медианы:
M=0,5•√(2a²+2b²-c²), где а, b и с - стороны треугольника, причем с- сторона, к которой проведена медиана.
DH=1/2•√(200+128-144)
DH²=184:4=46
CD=√(108+46)=√154