Sосн = Sпол - Sбок = 16√3. Поскольку треугольная пирамида правильная, то в основе лежит правильный треугольник. Следовательно, найдем сторону основания:
 - сторона основания.
- сторона основания.
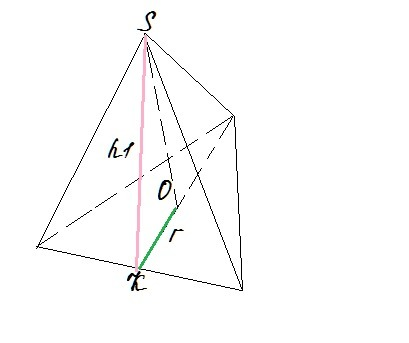
Радиус вписанной окружности основания: r = a/2√3 = 4/√3
Площадь грани: Sграни = Sбок : 3 = 32√3, тогда высота грани
h₁ = 2 * Sграни / a = 8√3
По т. Пифагора
h = √(h₁²-r²) = 4√105/3