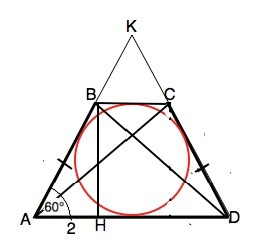
Обозначим вершины трапеции АВСD, АВ=СD, АD - ВС=4.
Опустим высоту ВН. Высота равнобедренной трапеции, опущенная из тупого угла, делит большее основание на отрезки, меньший из которых равен полуразности, больший - полусумме оснований.
АН=4:2=2.
ВН=АН•tg60°=2√3
ВН - диаметр вписанной окружности. r=√3.
Продолжив боковые стороны трапеции до их пересечения в точке К, получим равносторонний ∆ АКD с вписанной в него окружностью. Формула радиуса вписанной в правильный треугольник окржуности
r=a√3):6,
√3=a√3:6, откуда а=6. АD=АК=DК=6
НD=6-АН=4
Диагонали равнобедренной трапеции равны. АС=BD
ВD•BD=BD²
BD²=BH²+HD²=(2√3)²+4²=28