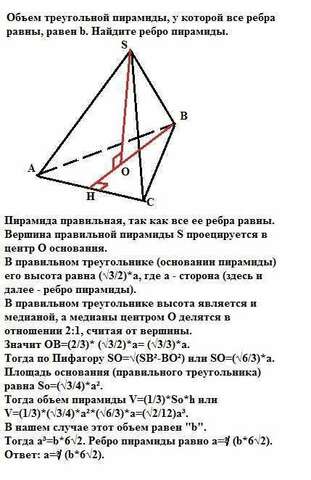
Пирамида правильная, так как все ее ребра равны.
Вершина правильной пирамиды S проецируется в центр О основания.
В правильном треугольнике (основании пирамиды) его высота равна (√3/2)*а, где а - сторона (здесь и далее - ребро пирамиды).
В правильном треугольнике высота является и медианой, а медианы центром О делятся в отношении 2:1, считая от вершины.
Значит ОВ=(2/3)* (√3/2)*а= (√3/3)*а.
Тогда по Пифагору SO=√(SB²-BO²) или SO=(√6/3)*а.
Площадь основания (правильного треугольника) равна So=(√3/4)*а².
Тогда объем пирамиды V=(1/3)*So*h или
V=(1/3)*(√3/4)*а²*(√6/3)*а=(√2/12)а³.
В нашем случае этот объем равен "b".
Тогда а³=b*6√2. Ребро пирамиды равно а=∛(b*6√2).
Ответ: а=∛(b*6√2).