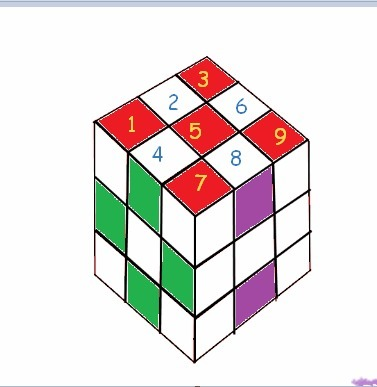
Поставим куб прямо перед собой.
Куб имеет 6 граней (6 сторон).
Если пронумеровать квадраты на гранях, из 3 × 3, всего 9, то:
1. На передней и задней от нас гранях нужно закрасить по 4 квадрата: 2; 4; 6; и 8.
2. На верхней и нижней гранях - закрасить по 5 квадратов 1;3; 5; 7 и 9.
3. На 2-х боковых гранях - закрасить по 2 квадрата: 2 и 8.
4+4+5+5+2+2=2(4+5+2)=22
Ответ: Наибольшее количество закрашенных по данному условию квадратов - 22.
Рисунок во вложении