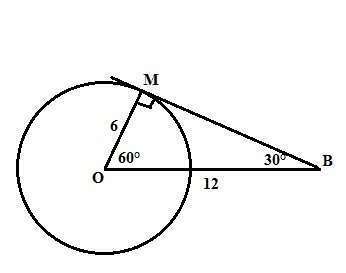
Радиус окружности перпендикулярен касательной в точке касания.
Треугольник ВОМ - прямоугольный с прямым углом М.
ОМ - гипотенуза. против угла 30 градусов лежит катет (радиус), равный 6. Значит гипотенуза равна 12. По Пифагору катет ВМ=√(12²-6²)=6√3. Площадь треугольника ВОМ равна (1/2)*6*6√3=18√3.
Ответ: Sbom=18√3 ед².