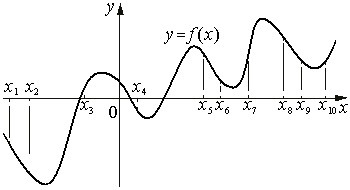На рисунке изображён график функции y=f(x). На оси абсцисс отмечены десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек производная функции f(x) положительна? (рис.1)
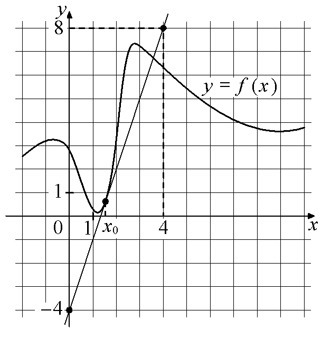
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. (рис.2)