264.
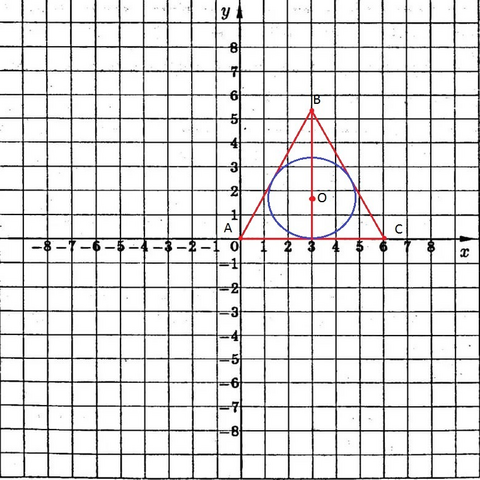
а) Пусть А(0;0), В(3;3√3), С(6;0).
1) Находим длины сторон ΔАВС:
|AB|=√((3-0)²+(√3-0)²)=√(9+27)=√36=6;
|BC|=√((6-3)²+(0-3√3)²)=√(9+27)=√36=6;
|AC|=√((6-0)²+(0-0)²)=√36=6.
Вывод: ΔАВС - равносторонний.
2) Радиус вписанной окружности можно найти по формуле:
r=a√3/6=6√3/6=√3.
3) Координаты точки центра вписанной окружности совпадают с центром тяжести равностороннего треугольника, который можно найти, как среднее арифметическое соответствующих координат вершин треугольника:
х0=(0+3+6)/3=9/3=3;
у0=(0+3√3+0)/3=√3;
Таким образом, центр вписанной окружности О(3;√3).
4) Составляем уравнение вписанной окружности:
(х-3)²+(у-√3)²=√3²;
(х-3)²+(у-√3)²=3.
Ответ: а) (х-3)²+(у-√3)²=3.
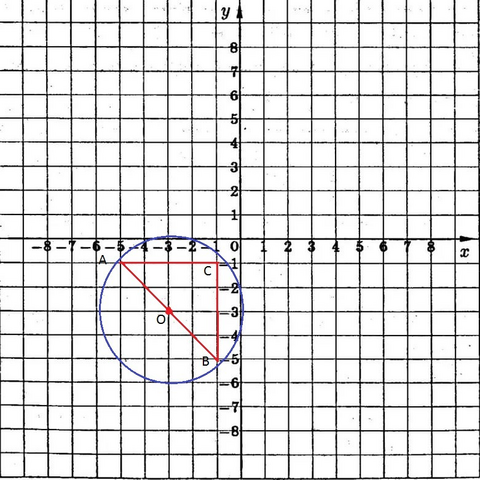
б) Пусть А(-5;-1), В(-1;-5), С(-1;-1).
1) ΔАВС - прямоугольный, равнобедренный.
Радиусом описанной окружности является половина гипотенузы АВ.
|АВ|=√((-1+5)²+(-5+1)²)=√32=4√2.
R=|AB|/2=4√2/2=2√2.
2) Находим центр окружности (середину гипотенузы АВ):
О((-5-1)/2; (-1-5)/2)=(-3;-3).
3) Составляем уравнение описанной окружности:
(х+3)²+(у+3)²=(2√2)²;
(х+3)²+(у+3)²=8.
Ответ: б) (х+3)²+(у+3)²=8.
265.
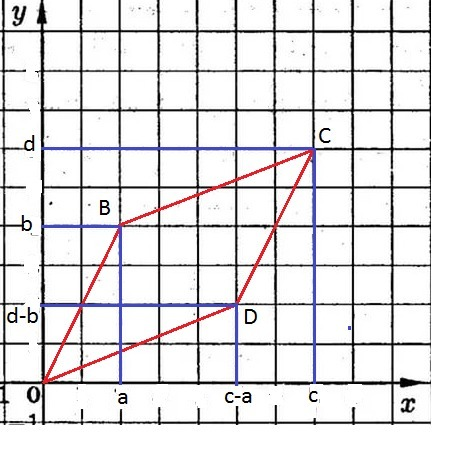
Пусть О(0;0), В(a;b), C(c;d), D-?
У параллелограмма противолежащие стороны равны, значит
|BC|=|AD|=√((c-a)²+(d-b)²).
Точка D имеет координаты (с-а; d-b).
Ответ: D(c-a;d-b).
266.
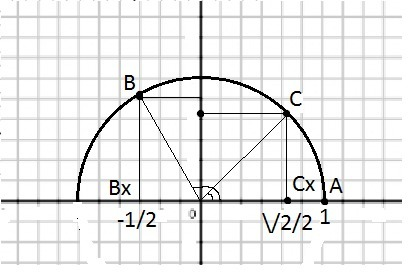
а) Рассмотрим ΔОСхС - прямоугольный, равнобедренный,
ОСх=√2/2, ОС=1, по т.Пифагора CCx=√(1²-(√2/2)²)=√(1-1/2)=√2/2,
sin∠AOC=CCx/OC=√2/2/1=√2/2 ⇒∠АОС=45°.
Ответ: sin∠AOC=√2/2.
б) Рассмотрим ΔВВхО - прямоугольный, ВхО=1/2, ВО=1, по т.Пифагора ВВх=√(1-1/4)=√3/2.
sin∠ВОВх=BBx/BO=√3/2/1=√3/2⇒∠BOBx=60°.
tg∠AOB=tg(180°-60°)=-tg60°=BBx/BxO=√3/2/(-1/2)=-√3.
Ответ: tg∠AOB=-√3.