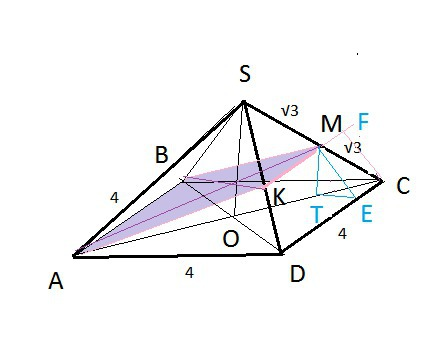
См. рисунок в приложении.
В основании пирамиды квадрат ABCD.
AB=BC=CD=AD=4.
O-центр квадрата.
АС=BD=4√2 - диагонали квадрата.
Из прямоугольного Δ SOC:
OC=AC/2=2√2
По теореме Пифагора
SO²=SC²-OC²=(2√3)²-(2√2)²=12-8=4;
SO=2.
Плоскость АВМ пересекает плоскость SCD по прямой МК || CD.
МК - средняя линия Δ SCD; МК=(1/2)СD=2.
Проводим МТ || SO; МТ=(1/2)SO=1.
Проводим ТЕ || AB. ТЕ⊥ CD ( AB⊥CD); ТЕ=1.
Треугольник МТЕ- прямоугольный. По теореме Пифагора МЕ=√2.
МЕ || CF, CF=√2 - искомое расстояние.