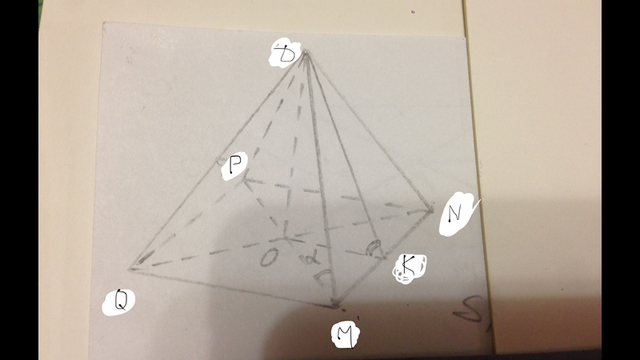
Получилась правильная пирамида DMNPQ. OD=8 см, MN=12 см.
DK⊥MN, OK⊥MN ⇒ OK=MQ/2=6 см - ответ в)
В тр-ке МDK DK²=OD²+OK²=8²+6²=100,
DK=10 см.
Так как основание высоты лежит в центре квадрата, то боковые грани одинаково наклонены к плоскости основания, значит боковые грани равны, равны апофемы, значит DK=10 см - ответ а).
S(MDN)=MN·DK/2=12·10/2=60 см² - ответ б).
Тр-ник MON - проекция тр-ка DMN на плоскость основания. Его площадь равна четверти площади квадрата MNPQ.
S(MON)=MN²/4=12²/4=36 см² - ответ б)