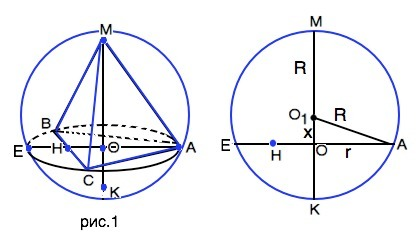
Обозначим пирамиду МАВС, центр шара О1, его диаметр МК.
Высота пирамиды МО=10 см. Сторона основания АВ=АС=ВС=9 см.
Основание пирамиды лежит в плоскости описанной вокруг него окружности с центром О. (см.рис.№1)
Радиус описанной окружности правильного треугольника равен а/√3: ОА=9/√3=3√3,
Рассмотрим схематический рисунок.
Пусть ОО1 -расстояние от центра шара до центра основания пирамиды равно х. Тогда R=10-х.
Из прямоугольного ∆ АОО1
R²= АО1*=OO1²+AO²=x²+27
R²=(10-x)²=100-20x+x²; R²=R² ⇒
x*²+27=100-20x+x² откуда
20х=73; х=3,65; ⇒R=10-3,65=6,35 см
По формуле объема шара V=4πR²/3= ≈1072,53 см³