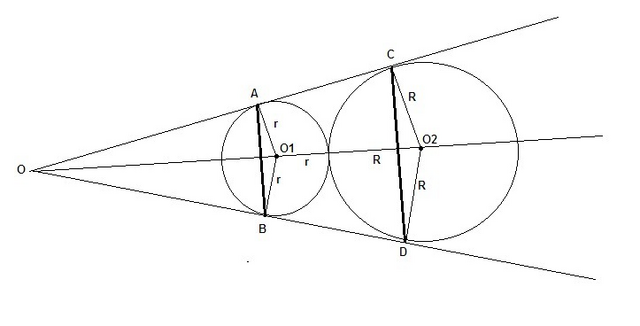
Очередная 26 задача из ОГЭ. Две окружности, вписанные в угол О, касаются друг друга...

Question

30 просмотров

Очередная 26 задача из ОГЭ.
Две окружности, вписанные в угол О, касаются друг друга внешним образом.
Точки A, B, C, D - точки касания окружностей и угла.
O1 и O2 - центры окружностей.
Их радиусы r = 15, R = 21.
Рисунок прилагается.
Требуется:
1) Определить, параллельны ли отрезки AB и CD.
(Мне кажется - не всегда!)
2) Найти наименьшее расстояние между этими отрезками.
Если они параллельны, то просто найти расстояние между ними.
В учебнике ответ 35, но мне кажется, что это опечатка и должно быть 15+21=36.
Как это решить?

Математика mefody66_zn (320k баллов) 12 Май, 18 | 30 просмотров

Дан 1 ответ

Правильный ответ

Отрезки AB и CD параллельны всегда - можно доказывать, рассматривая равенства всяких треугольников, но проще заметить, что имеется симметрия относительно биссектрисы угла О - если бы отрезки были не параллельны - не было бы симметрии.
обозначим MN - расстояние между AB и CD

далее проще использовать тригонометрию

обозначим половину угла О через $\alpha$
$sin a= \frac{R-r}{R+r}$

$\frac{r}{OB}=tg \alpha \\ OB= \frac{r}{tg \alpha } \\ \frac{OM}{OB}=cos \alpha \\ OM=OB*cos \alpha$

$\frac{R}{OD}=tg \alpha \\ OD= \frac{R}{tg \alpha } \\ \frac{ON}{OD}=cos \alpha \\ ON=OD*cos \alpha$
$OM=r* \frac{cos \alpha }{tg \alpha } = \frac{rcos^2 \alpha }{sin \alpha } \\ ON=R* \frac{cos \alpha }{tg \alpha } = \frac{Rcos^2 \alpha }{sin \alpha }$

$OM=r* \frac{cos \alpha }{tg \alpha } = \frac{rcos^2 \alpha }{sin \alpha } \\ ON-OM=(R-r) \frac{cos^2 \alpha }{sin \alpha } =(R-r) \frac{1-sin^2 \alpha }{sin \alpha }$

$ON-OM=(R-r) \frac{1- ( \frac{R-r}{R+r} )^{2} }{( \frac{R-r}{R+r} ) }= \frac{2r*2R}{R+r} = \frac{4rR}{R+r}$

$ON-OM=\frac{4rR}{R+r}= \frac{4*15*21}{21+15} = \frac{1260}{36} =35$

Ответ: 35

Ivanov2017_zn (2.9k баллов) 12 Май, 18