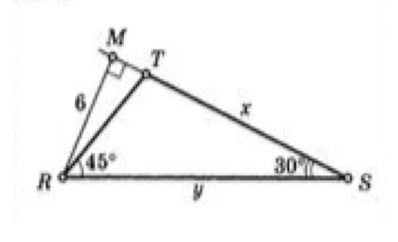
Дан тупоугольный ∆ RTS. Угол TRS=45° угол TSR=30° Высота RM, проведенная к стороне TS, равна 6.
Найти х и y ( стороны TS и RS)
* * *
RМ в прямоугольном треугольнике MRS - катет, противолежащий углу 30°. RS - гипотенуза этого треугольника и равна 2 MR. RS=12.
Угол RTS=(180°-45°-30°)=105°
По т.синусов RS/sin 105°=TS/sin45°
sin105°=(√3+1):2√2 ( по таблице с тригонометрическими функциями популярных углов)
TS:(√2/2)=12•2√2:(√3+1)
TS=(12•2√2*√2):(√3+1)
TS=24/((√3+1) или 8,7846