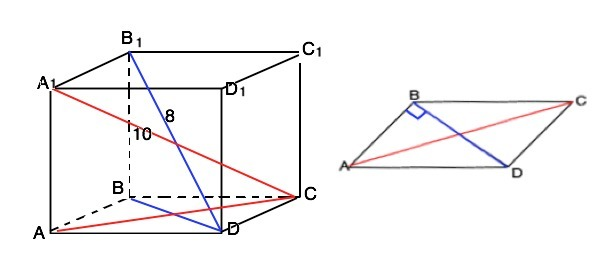
№3 Диагонали прямого параллелепипеда равны 8 м и 10 м. Стороны основания 5 м и 3 м. Найдите его объем.
———————
Объем параллелепипеда равен произведению площади основания на высоту.
Т.к. параллелепипед прямой, но не прямоугольный, то его ребра перпендикулярны основаниям, не прямоугольникам, а параллелограммам.
Пусть основание - параллелограмм АВСD, диагонали параллелепипеда В1Д=8, А1С=10.
Обозначим высоту параллелепипеда АА1=ВВ1= Н.
Из ∆ВВ1D диагональ основания ВD²=В1D²-Н²=64-Н²
Из ∆ АА1С диагональ основания АС²=А1С²-Н²=100-Н²
Известно, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. BD²+AC²=(AB²+AD²)•2
64-Н²+100-Н²=2•(9+25) откуда
2Н²=164-68
Н=√48=4√3
Диагональ ВD основания из ∆ ВВ1D=√(64-48)=√16=4
B ∆ ABD отношение сторон 3:4:5 - он "египетский" прямоугольный.
BD - перпендикулярна АВ и СD, ВD- высота параллелограмма.
S ABCD=ВD•AB=3•4=12 см²
V (пар)=S•H=12•4√3=48√3 м³
––––––––––––––––––––––––––––––––––––––––––––––––
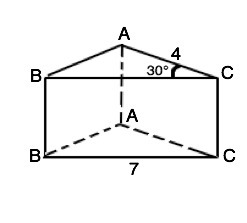
№ 6. Найдите объем прямой призмы АВСА1В1С1, если угол АСВ=30°, ВС=7 см, АС=4 см и наибольшая из площадей граней 28 см²
---------
Все грани прямой призмы - прямоугольники, ребра перпендикулярны основаниям. Высота прямой призмы равна её ребру.
ВВ1С1С –наибольшая из боковых граней: при равной высоте всех граней сторона ВС - наибольшая.
S=a•h, h=S:a. h=28:7=4см
V=S•h
S=AC•BC•sin30°:2=4•7•0,5:2=7 см²
V=7•4=28 см³