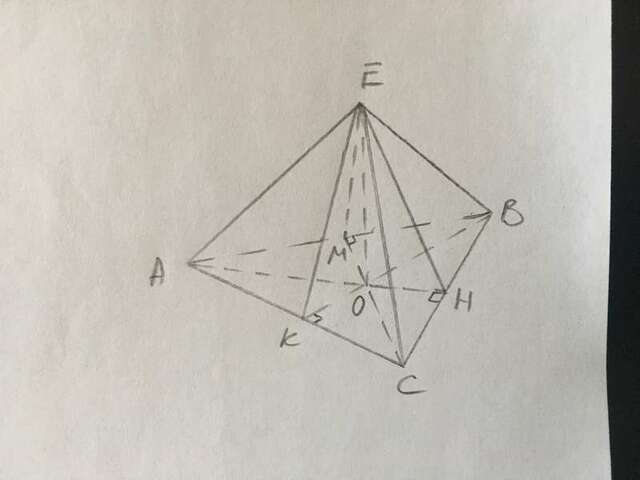
Так как пирамида правильная то боковые грани наклонены под одним углом к плоскости основания, поэтому основание высоты пирамиды лежит в центре вписанной окружности в правильный треугольник, лежащий в основании пирамиды.
ЕО=4 см, ∠ЕКО=45°, ОК=r - радиус вписанной окружности.
1. В прямоугольном тр-ке ЕОК острый угол равен 45°, значит он равнобедренный. ОК=ЕО=4 см.
В правильном треугольнике r=a√3/6 ⇒ a=6r/√3=2r√3.
АВ=а=2·4√3=8√3 - сторона основания.
2. Сечение, проходящее через середину высоты пирамиды параллельно плоскости основания, пересекает боковые рёбра посередине, значит сечение проходит по средним линиям боковых граней, которые равны половине сторон основания пирамиды.
Средняя линия равна m=АВ/2=4√3.
Площадь правильного тр-ка со стороной m:
S=m²√3/4=(4√3)²·√3/4=12√3 см² - площадь сечения.