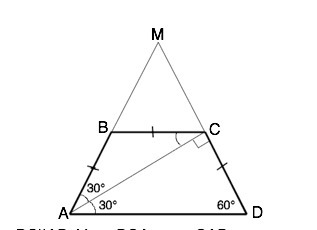
ВС||АВ. ∠ВСА=∠САD- накрестлежащие при пересечении параллельных прямых секущей. ∠ВАС=∠САD ( АС - биссектриса) ⇒ АВ=ВС=СD
Каждая из этих сторон равна 24√3:3=8√3 см
Один из вариантов решения:
AD=CD:sin30°=2•8√3=16√3 см
S ∆ ACD=CD•AD•sinCDA:2
S=4√3•16√3•0,5:2=48 см²
S ∆ACD=h•AD:2 ⇒h=2S:AD=96:16√3=2√3 см
Площадь трапеции равна произведению полусуммы оснований на высоту.
S ABCD=0,5•(BC+AD)•h=12√3•2√3=108 см²