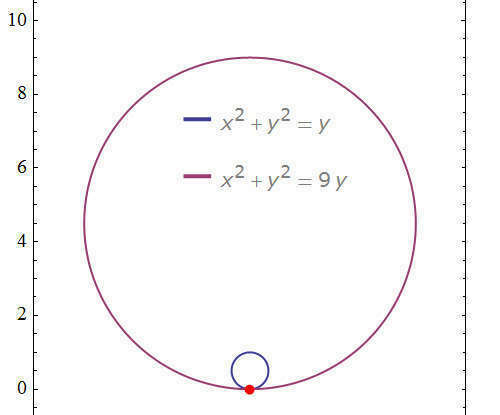
Построив график -- имеем два эллипса (окружности) Уравнение окружности имеет вид:

Первое, что мы делаем -- приводим к виду этого уравнения. В первом случае y переносим налево, чтобы собрать квадрат, прибавим и вычтем 1/4. Тогда:

Первая окружность имеет центр (a;b) -> (0;1/2) и радиус 1/2
Ровно аналогичную процедуру осуществляем со вторым уравнением эллипса. Имеем окружность с радиусом 4,5 и координатами центра (0;4,5)
График интересующей нас фигуры прикреплён в файле.
Чтобы найти площадь фигуры между линиями данных окружностей, найдём площади обеих и вычтем одну из другой.
В целом, тут даже неуместно стрелять из пушки по воробьям и составлять интегралы и их считать удовольствие очень среднее, с учётом известной формулы площади круга Pi*r^2. Радиусы-то у нас уже есть.
Тогда площадь большего круга S1=20,25*Pi
Площадь окружности, что поменьше S2=Pi/4
S1-S2=20*Pi
Ответ: 20*Pi