Helppp !! Помогите решить две задачи. Подробное решение с рисунком

Question

Дано ответов: 2

Правильный ответ

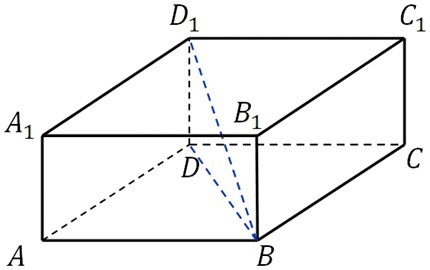
12) Дано: АВСDА₁В₁С₁D₁ - прямоугольный параллелепипед
АВСD -квадрат, ВD₁ =√3 - диагональ
∠DВD₁=60°
Найти: Vпараллелепипеда -?
Решение:
V=AB*AD*DD₁
1) В прямоуг.Δ BDD₁ можем найти DD₁, так нам известна его гипотенуза и острый угол:
cos∠DBD₁= DD₁ / BD₁ ⇒ DD₁=cos∠DBD₁*BD₁=1/2*√3=√3/2
2) Чтобы найти AB и AD, нужно узнать чему равна диагональ BD квадрата ABCD.
По теореме Пифагора BD²=BD₁²-DD₁²=(√3)²-(√3/2)²=3/2
найдем AB, так как AB=AD, то BD²=2AB² ⇒ AB²=BD² / 2=(3/2)² / 2=9/8
BD=√9/8
3) V= AB*AD*DD₁=√9/8*√9/8*√3/2=9/8*√3/2=9√3 / 16
Ответ:9√3 / 16

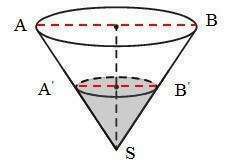
7) 1) V = 1/3 · h · Socн = 1/3 · h · π · (D/2)2

natalitaranuch_zn (8.1k баллов) 11 Май, 18

ssoxo_zn · Answer 1 · 2018-05-11T19:39:49+0000

1) В данном параллелепипеде АА1В1В - квадрат. СА1=√3, ∠СА1В=60°.
В прямоугольном тр-ке А1ВС А1В=А1С·cos60=√3/2.
ВС=А1С·sin60=√3·√3/2=3/2.
В квадрате АА1В1В АВ=АА1=d/√2=А1B/√2=√3/(2√2)=√6/4.
V=abc=АВ·ВС·АА1=АВ²·ВС=(√6/4)²·3/2=6·3/(16·2)=18/32=9/16 - это ответ.

2) ОН=h ⇒ OP=2h/3.
Прямоугольные треугольники АНО и КРО подобны т.к. ∠АОН - общий,
Значит КР/АН=ОР/ОН=2/3=k, кде k - коэффициент подобия.
R=AH. r=KP=AH·k=R·k.
OP=h·k.
Объём большого конуса: V=Sh/3=πR²h/3.
Объём налитой воды: V1=π·(R·k)²·h·k/3=πR²h·k³/3, значит
V=V1/k³=152/(2/3)³=152·3³/2³=513 мл.
Объём недостающей воды: V2=V-V1=513-152=361 мл - это ответ.

ssoxo_zn (34.9k баллов) 11 Май, 18