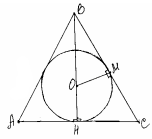
Периметр АВС= 2AB + AC
M – точка касания. Проведём ОМ. ОМ перпендикулярна ОС (как радиус, проведённый в точку касания).
Рассмотрим треуголиники ВНС и ВМО (угол ОВМ- общий , угол ОВМ= углу ВНС=90 град.)
ОМ/НС= ВМ/ВН ; НС= (ОМ*ВН)/ВМ
Из треуг.ВМО по теореме Пифагора
ВМ= √ОВ^2- ОМ^2 ; ВО=ВН-ОН
ВМ= √25--4=4
НС=(3*8)/4=6
Из треугольника НВС по теореме Пифагора ВС= √ВН^2*НС^2 = 10
Периметр треугольника АВС =20+12= 32 см
Ответ 32 см