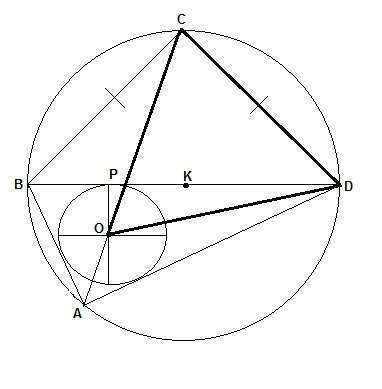
15. Рисунок я нарисовал.
Дано: AB = 3; BC = CD = 3√2; BD - диаметр опис. окружности.
Найти S(COD) (треугольник COD выделен жирным).
Решение: 1) Вписанный угол, опирающийся на диаметр - прямой.
BC = CD, значит BCD - равнобедренный и прямоугольный треугольник.
BC = CD = 3√2; BD = BC*√2 = 3√2*√2 = 6
AB = 3; BD = 6 = AB*2. Катет против угла 30° = половине гипотенузы.
Значит, Интересно, у меня случайно получилось, что О - центр окружности, вписанной в ABD, находится на диагонали AC?
Или это всегда так, и это можно доказать?
Как известно, центр вписанной в треугольник окружности находится в точке пересечения биссектрис.
Значит, DO - биссектриса Треугольник COD - равнобедренный и один из его углов равен 60°.
Значит, он равносторонний. CD = OC = OD = 3√2.
S(COD) = a^2*√3/4 = 9*2*√3/4 = 4,5√3
16.
{ yx^2 - y^2 + 5x^2 = 14y + 45
{ x ≥ -3
{ x = y - a
Преобразуем 1 уравнение
x^2*(y+5) = y^2 + 14y + 45 = (y+5)(y+9)
При y = -5 обе части обращаются в 0, это решение при любом х.
То есть это бесконечное множество решений.
Нам это не подходит, значит, y =/= -5.
Сокращаем y+5
x^2 = y + 9
y = x^2 - 9
Получаем систему
{ y = x^2 - 9
{ x ≥ -3
{ y = x + a
Подставляем 3 уравнение в 1 уравнение
x^2 - 9 = x + a
x^2 - x - (a+9) = 0
D = 1 - 4(-(a+9)) = 4a + 37
x1 = (1 - √(4a+37))/2
x2 = (1 + √(4a+37))/2
Чтобы было два корня, должны соблюдаться два условия:
{ 4a + 37 > 0; отсюда a > -37/4 = -9,25
{ (1 - √(4a+37))/2 ≥ -3
Ясно, что x2 > x1, поэтому достаточно проверить, что x1 ≥ -3
1 - √(4a+37) ≥ -6
√(4a+37) ≤ 7
4a + 37 ≤ 49
a ≤ (49 - 37)/4 = 12/4 = 3
Решение: a ∈ (-9,25; 3]
Осталось проверить условие y =/= -5
y = x + a =/= -5
x =/= -a - 5
Проверяем оба корня
x1 = (1 - √(4a+37))/2 =/= -a - 5
1 - √(4a+37) =/= -2a - 10
√(4a+37) =/= 2a + 11
4a + 37 =/= 4a^2 + 44a + 121
4a^2 + 40a + 74 =/= 0
2a^2 + 20a + 37 =/= 0
D = 20^2 - 4*2*37 = 400 - 8*37 = 400 - 296 = 104 = (2√26)^2
a1 =/= (-20 - 2√26)/4 = -5 - √26/2 ~ -7,55 > -37/4
a2 =/= (-20+2√26)/4 = -5 + √26/2 ~ -1,9 > -37/4
Оба корня попадают в решение, поэтому
Ответ: a ∈ (-37/4; -5 - √26/2) U (-5 - √26/2; -5 + √26/2) U (-5 + √26/2; 3]