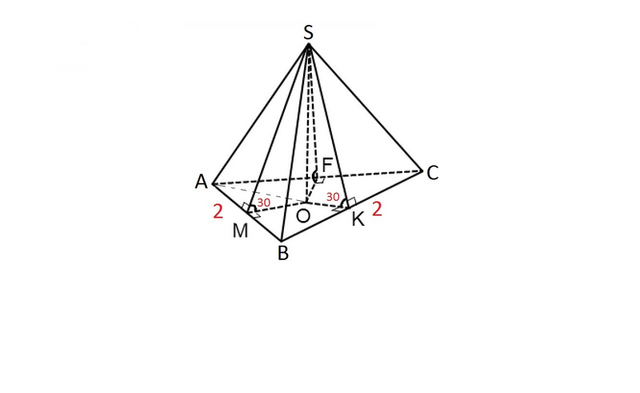
правильная треугольная пирамида

высота

см


?

правильная треугольная пирамида

⊥

Δ

равносторонний


см²


см²

где

длина апофемы

см
Δ

равносторонний

⊥


см
Δ

прямоугольный
По теореме Пифагора найдем AK:




см

( по свойству медиан)

см

⊥

Δ

прямоугольный





см

см²

см ²
Ответ: 2+√3 см²