Первое плз, с подробным объяснением (срочно)

Question

Дан 1 ответ

NataliaBorisevich_zn · Answer 1 · 2018-05-11T17:23:54+0000

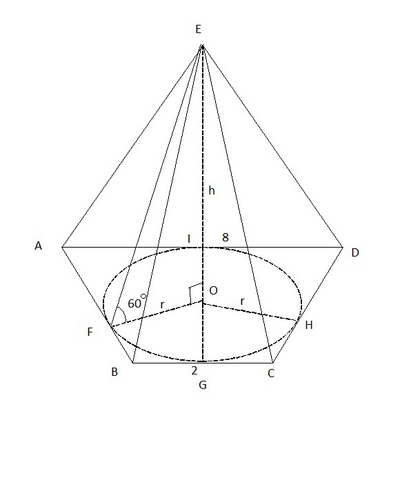
1) Т.к. все боковые грани расположены под одним углом в основанию, то высота падает в центр вписанной в основание окружности.
Построим линейный угол двугранного угла ∠EABC, для этого опустим перпендикуляр из т.O к ребру AB, EF⊥AB по т. о трех перпендикулярах, где EF - наклонная, OF - проекция, EF⊥AB и OF⊥AB ⇒∠EFO - линейный угол двугранного угла = 60°.

2) Радиус вписанной в трапецию окружности
$r= \frac{ \sqrt{AD*BC}}{2} = \frac{ \sqrt{2*8}}{2} = \frac{4}{2} = 2$ (см)

3) ΔEOF - прямоугольный, EO - высота. Обозначим высоту h., ∠EFO обозначим α
$h = \frac{r}{tg \alpha } = \frac{2}{tg60}= \frac{2}{ \sqrt{3} }$ (см)
$FE = \frac{r}{cos60} = \frac{2}{ \frac{1}{2} } = 4$ (см)

4) ΔEOF = ΔEOG = ΔEOH = ΔEOI, т.к. они все прямоугольные, у них общая высота, и одинаковый угол между гипотенузой и нижним катетом (по условию все боковые грани находятся по углом 60° к основанию) ⇒ у них равные гипотенузы, которые являются высотами боковых граней, по ТТП. (теорема и трех перпендикулярах)

5) т.к. трапеция равнобедренная AB = CD и из 4) ⇒ EF = EH ⇒
$S_{ABE} = S_{CDE} = \frac{1}{2} *EF*AB$ , необходимо найти AB

Опустим в основании высоту BB1
AB1 = (AD - BC)/2 = (8-2)/2 = 3
$BB1 = \sqrt{BC*AD} = \sqrt2*8} = 4$
$AB = \sqrt{ AB1^{2} + BB1^{2} } = \sqrt{9+16} = 5$ (см)
$S_{ABE} = S_{CDE} = \frac{1}{2} *EF*AB = \frac{1}{2} *4*5 = 10$ (см²)

6) $S_{BEC} = 1/2*EG*BC = 1/2*4*2 = 4$ (см²)
7) $S_{AED} = 1/2*EI*AD = 1/2*4*8 = 16$ (см²)

8)
Площадь боковой поверхности
$S = S_{AED} + S_{BEC} + 2*S_{ABE}$
$= 16 + 4 + 2*10 = 40$ (см²)