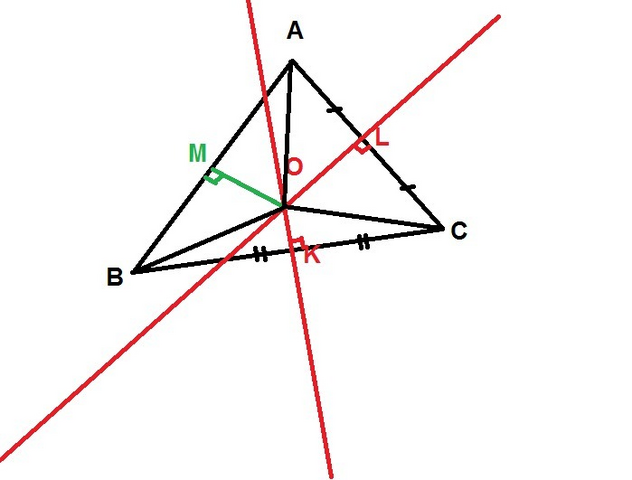
Пусть дан треугольник ABC (рисунок прилагается). Проведем серединные перпендикуляры к AC и BC. Они пересекутся в точке O (они не могут быть параллельными, так как иначе AC и BC были бы параллельными, либо совпадали).
Теперь опустим из O высоту OM на AB и докажем, что она является и медианой.
Для треугольника BOC:
OK - медиана и высота, значит BO = OC (треугольник BOC равнобедренный).
Для треугольника AOC:
OL - медиана и высота, значит AO = OC (треугольник AOC равнобедренный)
Отсюда AO=BO. Значит OM - высота равнобедренного треугольника. Отсюда OM - медиана.
Что и требовалось доказать.