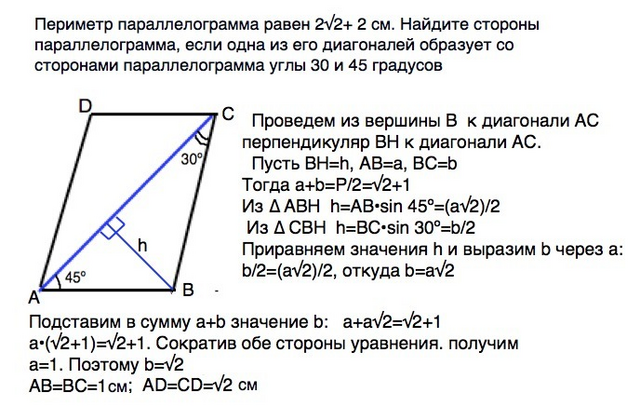
Проведем из вершины В к диагонали АС перпендикуляр ВН.
Пусть ВН=h, АВ=а, BC=b
Тогда a+b=P/2=√2+1
Из ∆ АВН h=AB•sin 45º=(a√2)/2
Из ∆ СВН h=BC•sin 30º=b/2
Приравняем значения h и выразим b через а:
b/2=(a√2)/2, откуда b=a√2
Подставим в сумму а+b значение b:
a+a√2=√2+1⇒
a•(√2+1)=√2+1. Сократив обе стороны уравнения на √2+1. получим
a=1. Поэтому b=√2
АВ=CD=1 см, ВС=AD=√2 см