Решим задачу в более общем случае - рассмотрим все возможные варианты для 4 попыток.
Введем обозначения = М и Д.
1. Полная вероятность события всегда равна 1.
Для одной попытки - всего вариантов - М+Д = n = 12+15 = 27.
Вариантов - для М = m = 12.
Вероятность по классической формуле Р(М) = p = m/n = 12/27 = 4/9 ≈ 0.444 = 44.4% - один билет и он достанется мальчику.
Девочка - НЕ мальчик. Р(Д) = q = 15/27 = 5/9 ≈ 55,6% - билет достанется девочке.
Вероятность события - Р(А) = p+`q = 4/9 + 5/9 = 1 - других вариантов нет.
А теперь таких билетов стало 4.
Полная вероятность такого события рассчитывается по формуле разложения бинома четвертой степени.
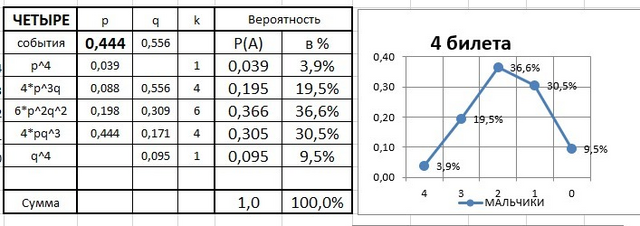
Р(А) = (p+q)⁴ = p⁴ + 4*p³q + 6*p²q² + 4*pq³ + q⁴ = 1= 100%.
Важно! Вероятность событий "ИЛИ" - суммируются, а событий "И" - умножаются.
Важно! Каждое слагаемое описывает возможный вариант -
p⁴ - все 4 билета достанутся мальчикам ИЛИ
q⁴ - все 4 билета достанутся девочкам ИЛИ
6*p²q² - два мальчика и две девочки - это как раз наша задача - ИЛИ
4*p³q ИЛИ 4*pq³ - еще два варианта событий.
Расчет к задаче приведен в таблице в приложении.
Получаем для варианта - Р(м²д²) = Р(А)

Р(А)≈0,366 = 36,6% - два мальчика и две девочки - ОТВЕТ
А из таблицы можно найти вероятности и других событий.