Обычно функции y = [x] и y = {x} определятся так:
y = [x] - наибольшее целое число, не превосходящее x
y = {x} ≡ x - [x] - дробная часть x
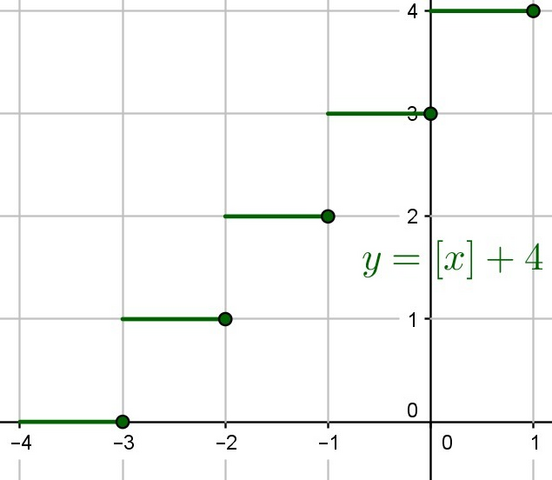
График функции y = [x] - набор ступенек, y = n, если n <= x < n + 1 . График y = [x] + 4 - тот же график, но сдвинутый на 4 единицы вверх.<br>
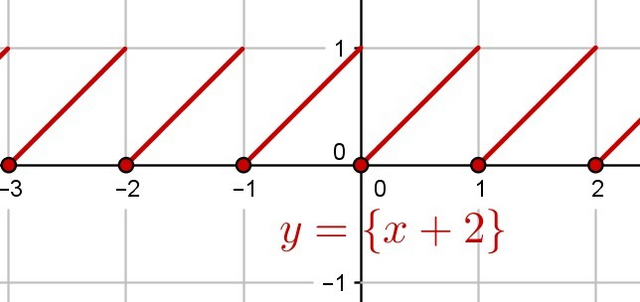
График функции y = {x} на полуинтервале [0, 1) совпадает с y = x, а дальше повторяется с периодом 1. y = {x + 2} ничем не отличается, так как прибавление целого числа никак не меняется дробную часть. Можно понять это и по-другому: y = {x + 2} это график y = {x}, сдвинутый на 2 единицы влево, но так как функция периодична с периодом 1, ничего не изменится.