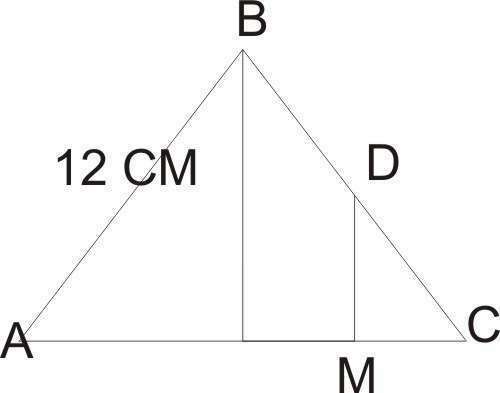
Δ АВС равносторонний, значит АВ=ВС=АС=12см
<А=<В=<С = 60°</p>
Построим высоту ВК, которая будет являться и медианой и биссектрисой ΔАВС
⇒АК=КС = ½АС = 6см
∢ΔВКС - прямоугольный
DM является средней линией ΔВКС, т,к. ВК параллельно DM, т.D середина отрезка ВС ⇒ и т.М середина стороны КС
КМ=МС=½КС = ½*6=3см
АМ=АС - МС = 12-3 = 9 см
Ответ АМ = 9 см