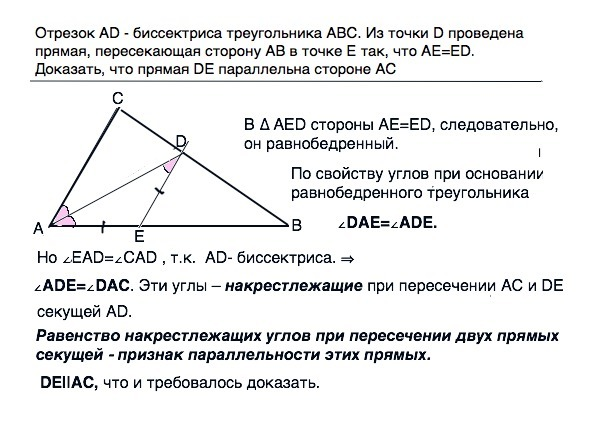
В ∆ АЕD стороны AE=ED, следовательно, он равнобедренный.
По свойству углов при основании равнобедренного треугольника
∠DAE=∠ADE.
Но ∠EАD=∠CAD , т.к. AD- биссектриса.
⇒ ∠АDE=∠DAC. Эти углы – накрестлежащие при пересечении АС и DE секущей AD.
Равенство накрестлежащих углов при пересечении двух прямых секущей - признак параллельности этих прямых.
DE||АС, что и требовалось доказать.