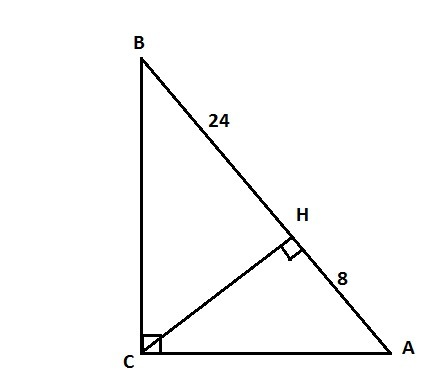
1) Пусть ΔАВС - прямоугольный, ∠С=90°, СН - высота, ВН=24 см, АН=8 см.
2) Высоту прямоугольного треугольника, проведенную к гипотенузе можно найти по формуле: CH²=BH*AH.
CH²=24*8=192;
CH=8√3 см.
3) ΔАНС - прямоугольный, СН=8√3 см, АН=8 см, по т.Пифагора
АС=√(СН²+АН²)=√(192+64)=√256=16 (см).
4) ΔВНС - прямоугольный, СН=8√3 см, ВН=24 см, по т.Пифагора
ВС=√(ВН²+СН²)=√(192+576)=√768=16√3 (см).
5) АВ=ВН+АН=24+8=32 (см).
Ответ: 16 см, 16√3 см, 32 см.