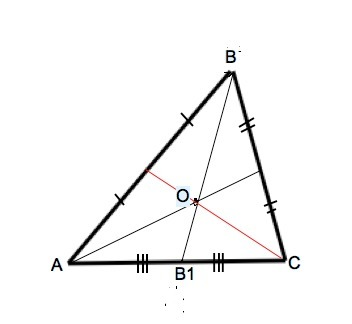
Есть теорема о том, что Медианы треугольника делят треугольник на 6 равновеликих треугольников. Поэтому можно сразу сказать, что искомая площадь равна 1/6 площади исходного треугольника.
_______
В ∆АВВ1 и ∆В1ВС основания равны, высота общая. По формуле S=a•h/2 их площади равны. ⇒ S∆ ABB1=1/2 S∆ ABC.
По т. о медианах треугольника точка пересечения двух его медиан делит каждую из этих медиан в отношении 2:1, считая от вершины треугольника.
⇒ в ∆ АОВ1 основание ОВ1 в два раза меньше основания ВО в ∆ АОВ.
Высоты обоих треугольников, проведенные к основаниям, совпадают. Отношение площадей треугольников с равными высотами равно отношению длин их оснований.
⇒S∆АОВ1:S∆AOB=1/2 , и площадь треугольника АОВ1 равна половине площади ∆ АОВ, или 1/3 половины площади ∆ АВО.
А т.к. S ∆ ABB1=1/2 S ∆ ABC, то S ∆ АОВ1=1/6 площади ∆ АВС=Q/6