ДУМАЕМ
Достаточно знать коэффициенты наклона - tg a = k.
tg β = (k₂ - k₁)/(1 + k₁*k₂)
РЕШЕНИЕ
Уравнение прямой АВ.
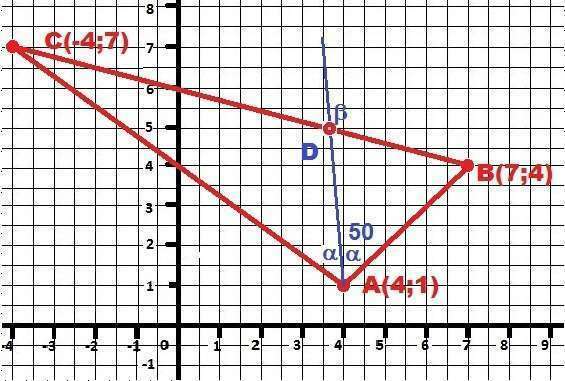
k1= (By - Ay)/(Bx - Ax) = 1 - (запоминаем), y(АВ) = x - 3 - (не нужно)
Уравнение прямой АС.
k2 = -3/4 - (запоминаем), y(AC) = -3/4*x + 4 - (не нужно)
Угол между прямыми АВ и АС - (2α)
tg(2α) = (-0.75-1)/(1+(-0.75)*1) = -7
Находим полный угол A = 2*α = arctg(-7) = -1.43 = 100°
Угол наклона биссектрисы = 45 + 50 = 95°
k3 = tg95° = tg (1.658 = - 11.4
Уравнение биссектрисы - y(AD) = -11.4*x + ???
Уравнение прямой ВС - у(ВС) = - 3/11*х + 6
k4 = - 3/11 = -0.2727
И, наконец, угол между биссектрисой и стороной.
k5 = 1.217
β =π - arctg(1.217 =180° - 70° = 110° - ОТВЕТ