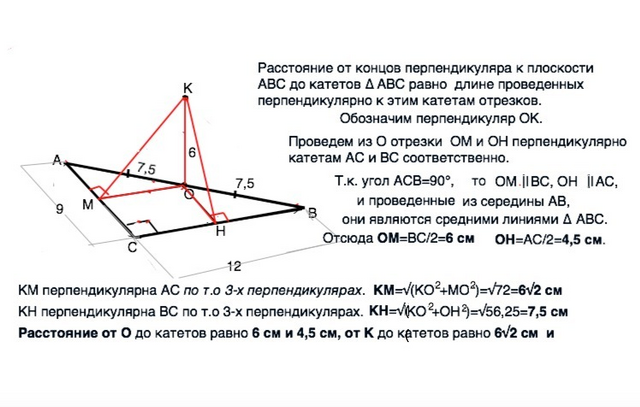
Расстояние от концов перпендикуляра к плоскости АВС до катетов
∆ АВС равно длине проведенных перпендикулярно к этим катетам отрезков.
Обозначим перпендикуляр ОК.
Проведем из О отрезки ОМ и ОН перпендикулярно катетам АС и ВС соответственно.
Т.к. угол АСВ=90°, ОМ║ВС, ОН ║АС, и проведенные из середины АВ, они являются средними линиями ∆ АВС.
Отсюда ОМ=ВС/2=6 см
ОН=АС/2=4,5 см.
КМ перпендикулярна АС по т.о 3-х перпендикулярах.
КМ=√(КО²+МО²)=√72=6√2 см
КН перпендикулярна ВС по т.о 3-х перпендикулярах.
КН=√KO²+OH²)=√56,25=7,5 см
Расстояние от О до катетов равно 6 см и 4,5 см, от К до катетов равно 6√2 см и 7,5 см.