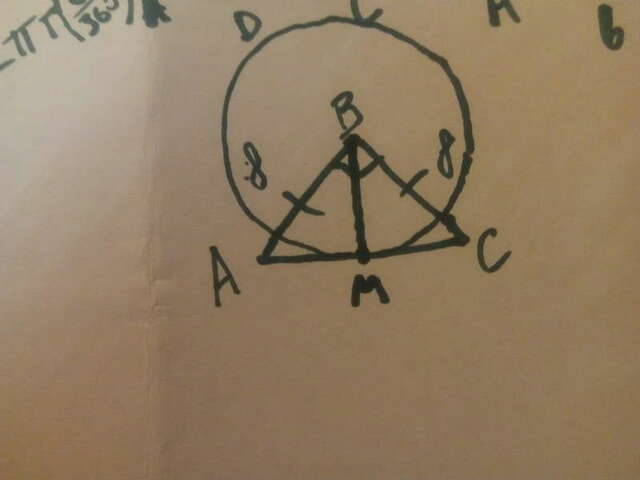
Найдём гипатенузу АС треугольника АВС:
по теореме Пифагора считаем
АС²=АВ²+ВС²
АС²=8²+8²
АС²=64+64=128
АС=√128=8√2 (см).
проведём медиану ВМ, который, кстати, будет являться ещё и радиусом окружности, который нам позже понадобится. В равнобедренном треугольнике медиана будет делить сторону АС на две равных части,
тогда АМ=8√2/2=4√2 (см).
медиана ВМ есть ещё и биссектриса,
так что АМ=ВМ=4√2 (см).
теперь используем формулу для нахождения дуги окружности:
L=2πr(ø/360°), где π-число пи; ø-центральный угол.
подставляем значения:
L=2π*BM(уголАВС/360°)
L=2π*4√2(90°/360°)=2π√2≈8.885 (см).
Ответ: длина дуги, ограниченная треугольником АВС=2π√2≈8.885 см.