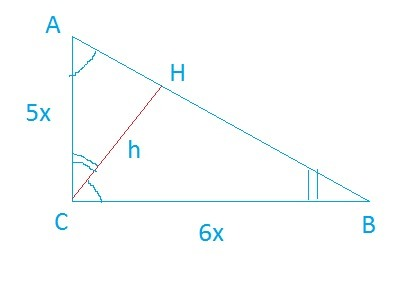
Пусть АС=5х, ВС=6х.
АС:ВС=5х:6х=5:6
Треугольники АСН и СВН подобны по двум углам.
Из подобия:
5х:6x=AH:BН
AH:BН=5:6
6АН=5ВН ⇒ ВН=1,2АН
а)BH-AH=11 см
1,2АН-АН=11
0,2АН=11
АН=55
ВН=1,2·55=66
АВ=АН+ВН=55+66=121
б)2AH+BH=43см
2АН+1,2АН=43
3,2АН=43
АН=43/3,2=13,4375
ВН=1,2·(43/3,2)
ВН=16,125
АВ=АН+НВ=13,4375+16,125=29,5625
в)2AH-BH=14см
2АН-1,2АН=14
0,8АН=14
АН=17,5
ВН=1,2·17,5=21
АВ=АН+НВ=17,5+21=38,5