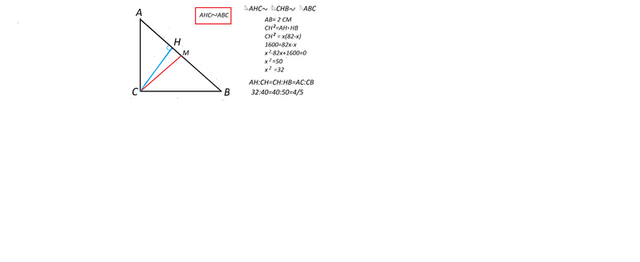
Высота, опущенная из вершины прямого угла на гипотенузу, делит прямоугольный треугольник на подобные треугольники.
Гипотенуза прямоугольного треугольника равна длине двух его медиан.
Пусть коэффициент данного по условию отношения высоты и медианы будет 1.
Тогда высота равна 40, медиана 41, гипотенуза 2*41=82
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Примем отрезок АН гипотенузы за х, НВ тогда 82-х
Квадрат высоты равен произведению отрезков АН и НВ
СН²=АН*НВ
1600=х(82-х)
х²-82х+1600=0
Решив квадратное уравнение, найдем два значения х=50 и х=32.
АН, как более короткий отрезок, равен 32,
НВ=50
Треугольники АНС, СНВ и АВС подобны .
И отношение их катетов одинаково.
Найдем отношение известных катетов в треугольниках АНС и СНВ. АН:СН=СН:НВ=4:5
АС:СВ=4/5
------------------------------
Но всегда простое решение - лучше сложного.
Вариант решения:
Основа решения:
Гипотенуза прямоугольного треугольника равна длине двух его медиан.
Между медианой и высотой образовался прямоугольный треугольник с гипотенузой СМ=41 и катетом СН=40.
По т.Пифагора отрезок гипотенузы НМ=9.
И тогда катет АН треугольника АНС относится к соответственному катету СН подобного ему треугольника СНВ как АН:НС=32:40=4/5
--------------
И вариант третий - если знать, что в треугольнике с гипотенузой 41, и катетом 40 второй катет равен 9 ( одна из троек Пифагора)- позволяет обойтись самым минимумом вычислений.