Используем свойство степеней: 15^x = 3^x*5^x, 3^(x+1) = 3*3^x,
5^(x+1) =5*5^x.
Тогда исходное неравенство запишем в виде:
В числителе вынесем за скобки в первой паре 3^x, а во второй паре 5:
Ещё раз вынесем за скобки 5^x-3:
Определяем точки, в которых числитель и знаменатель обращаются в нуль.
5^x-3 = 0, 5^x = 3, 
≈ 0,682606.
3^x-5 = 0, 3^x = 5, 
≈ 1,464974.
-x = 0, x = 0.
x-2 = 0, x = 2.
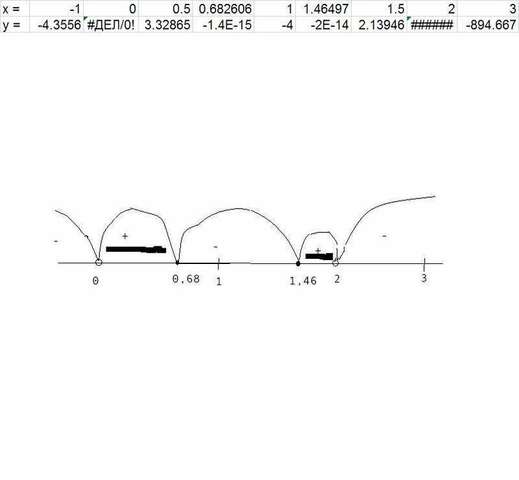
Применяем метод интервалов.
Рисуем ось Х и расставляем точки, в которых числитель и знаменатель обращаются в нуль (рисунок в приложении).
