3. Пусть ABCDE — выпуклый пятиугольник такой, что AB= AE =CD =1, ∠ABC =∠DEA=90◦ и BC + DE...

Question

3. Пусть ABCDE — выпуклый пятиугольник такой, что AB= AE =CD =1, ∠ABC =∠DEA=90◦
и BC + DE = 1. Вычислите площадь пятиугольника ABCDE.

Answer 1

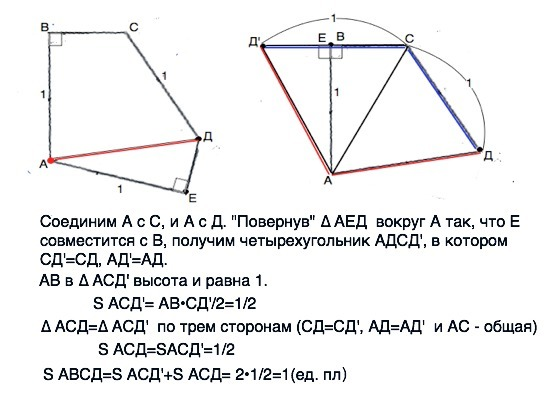
Соединим А с С, и А с Д. "Повернув" ∆ АЕД  вокруг А так, что Е совместится с В, получим четырехугольник АДСД', в котором СД'=СД, АД'=АД.

АВ в ∆ АСД' высота и равна 1. СД’=ВС+ДЕ=1 

 S АСД'= АВ•СД'=1•1:2=1/2

 ∆ АСД=∆ АСД'  по трем сторонам (СД=СД', АД=АД'  и АС - общая)

S АСД=SАСД'=1/2

S АВСД=S АСД'+S АСД= 2•1/2=1(ед. площади)

---