Плиииииииз, пожалуйста всё облазил ничего не нашёл. Поставил все баллы. Сумма Углов При...

Question

Плиииииииз, пожалуйста всё облазил ничего не нашёл. Поставил все баллы.

Сумма Углов При основании трапеции равна 90 градусов. Докажите, что высота трапеции есть среднее пропорциональное между проекциями её боковых сторон на основание..
Плиз если можно с чертежеом, но обязательно Дано, Решение и ТП.

Answer 1

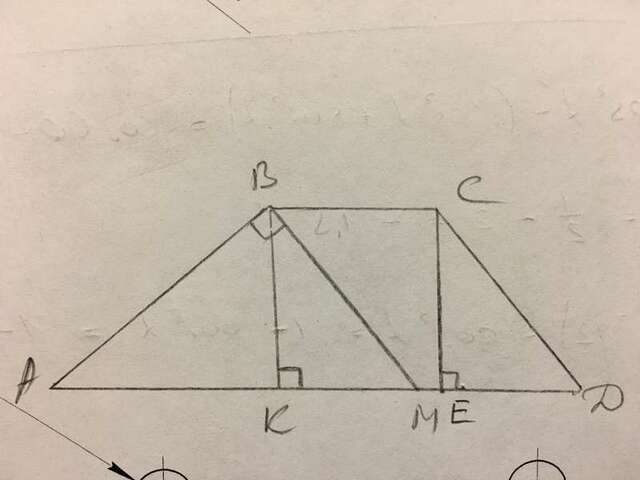
В трапеции АВСД проведём ВМ║СД. 
В полученном треугольнике АВМ ∠ВМА=∠СДА, значит ∠ВМА+∠ВАМ=90°, значит ∠АВМ=90°.
Высота ВК⊥АМ.
ВМ=СД, значит КМ=ЕД, значит АК и КМ - проекции боковых сторон трапеции на большее основание.
В прямоугольном треугольнике высота, проведённая к гипотенузе, делит его на два треугольника, подобные ему и друг другу, значит ВК/АК=КМ/ВК ⇒ ВК²=АК·КМ.
ВК=√(АК·ЕД).
Доказано.

---

Comments

Прослезился, думал уже ничего. Спасибо, пойду ещё баллы зарабатывать на 3 задания.

---

Спасибо ещё раз

---

Да, пожалуйста. Баллы можно и впрок зарабатывать ;)